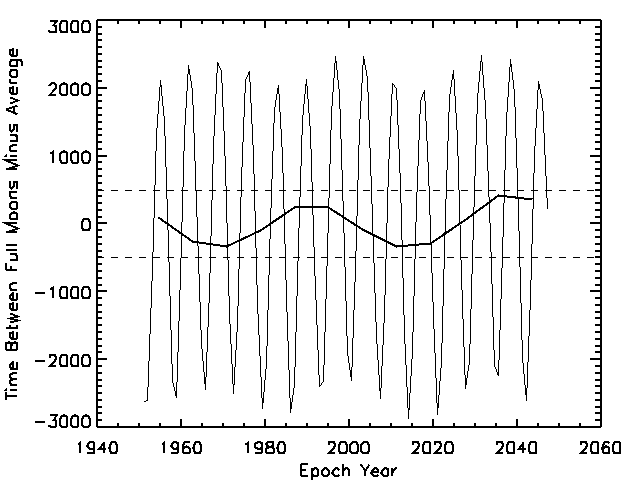
Figure 1: Time (in seconds) between successive full moons,
minus the mean. The thin line is the 1-year average; the thick line
is the 8-year average. The two dashed lines show +/- 500 seconds.
I show that there is nothing special about the past five or ten years of earth and sun motion. I have tabulated the epochs of full moons and vernal equinoxes for epochs between 1950 and 2050, with a precision of better than 10 seconds. The times between these events show no remarkable trends. If anything, the time range between 1995 and 2003 is more unremarkable than other times in the same range.
It has been claimed by Leider and "Mike Lob" that over the period of the past few years there has been an alarming trend in the times of full moons and vernal equinoxes, which suggest somehow a coming catastrophy and/or manipulation of the global time system. I have tabulated the epochs of these events for the years 1950-2050, and nothing particularly remarkable is apparent.
The times of full moon and vernal equinox were tabulated using an iterative procedure. The definition of the full moon is that the sun and moon must be 180 degrees apart, as measured in apparent earth-centered ecliptic longitude. This equation is,
lambda_moon - lambda_sun + 180 = 0 (Full Moon)
where lambda_moon and lambda_sun are the true ecliptic longitudes of the sun and moon, measured in degrees. The definition of the vernal equinox is that the apparent position of sun is at the first point of Aries, or equivalently, at exactly zero apparent ecliptic longitude. This equation is,
lambda_sun = 0 (Vernal Equinox)
These two equations are solved by an iterative process. A trial solution is made over a range of several days. A crude zero-crossing is found, a new bracketing range is determined, and a new trial solution is generated. The iteration is stopped when the bracket is less than 10 seconds.
To compute the apparent ecliptic longitude of the sun and moon, their positions are first, referred to the mean equator and equinox of the epoch J2000.0. The coordinates are rotated into the true equator and equinox of date, and then to the true ecliptic of date. The light travel time is accounted for, but planetary aberration is ignored, as being small.
The tabulation programs (see appendix) construct data files contain the epochs of full moon and vernal equinox. The columns are: (1) Epoch, expressed as Julian Day; (2) Calendar date; (3) Calendar time (UTC); (4) Difference from previous value. The files are:
In the portion of overlap, the values I have tabulated agree to within 1 minute with the USNO tabulations (moon, equinoxes), and also within ~1 minute with those derived from Meeus. Both of these sites only quote the epoch time to 1-minute precisions, so no better can be hoped for.
Thus, I can say that using my tabulation is essentially equivalent to the tabulations of the USNO and Meeus which Lob has relied upon. The benefit of my tabulations are that they are taken to a higher precision (10 seconds), and they are given in terms of Julian days which are easy to process further.
Here is a plot of the times between full moon, after subtracting the mean value. The signal clearly has many harmonic terms, which are apparent in the the figure. Two different averaging timescales are shown (1-year and 8-year), but neither reveals any dramatic trends. In fact, the trend over the 2000-2003 timescale is benign, compared to other time ranges, and in the opposite direction than that quoted by Lob.

Figure 1: Time (in seconds) between successive full moons,
minus the mean. The thin line is the 1-year average; the thick line
is the 8-year average. The two dashed lines show +/- 500 seconds.
A second plot shows the times between successive vernal equinoxes, again minus the mean value. Here, the 1-year signal is much more noisy, but also at a much smaller level compared to the full moon time series. I believe that most of this variation is due to earth nutation. The 7-year averaged signal has an r.m.s. of about +/-100 seconds. Again, the trend identified by Lob is not seen, and in fact the time between 2000-2003 shows less variability than during 1960-1980.

Figure 1: Time (in seconds) between successive vernal
equinoxes, minus the mean. The thin line are the 1-year values; the
thick line is the 7-year average.
Both signals are highly variable, and especially in the case of the moon, contain strong high frequency harmonics. One must take some care in the averaging of intervals. It is my opinion that Lob has averaged the signal over several different, incompatible, timescales, and has thus come to inappropriate conclusions. If you look at short timescales, of course you will see large variations (i.e. the rapid moon variations); and if you average at long timescales you will see smaller variations. These are exactly the effects that Lob sees. When averaged at consistent levels across the board the time range 1995-2003 are highly unremarkable.
The programs to tabulate the epochs of full moon and vernal equinox are written in IDL, the Interactive Data Language, and requires several tools and tables also available from my IDL library page. The files are: