To my knowledge the properties of the postulated flux loop are not
determined precisely, so I will design an approximation which appears
reasonable. For simplicity, I will construct the ![]() - and
- and
![]() -components separately, and then at time
-components separately, and then at time ![]() form the product
form the product
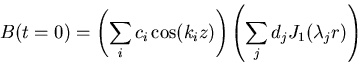 |
(25) |
The flux loop appears to be very compact in both the ![]() - and
- and
![]() -directions. Unfortunately compact functions are often the most
difficult to approximate with Fourier-type series, but it is possible.
In the
-directions. Unfortunately compact functions are often the most
difficult to approximate with Fourier-type series, but it is possible.
In the ![]() direction I found that a Gaussian profile is most
straightforward to construct, which is achieved by generating
coefficients
direction I found that a Gaussian profile is most
straightforward to construct, which is achieved by generating
coefficients ![]() with a broad Gaussian distribution:
with a broad Gaussian distribution:
![]() , and with
, and with ![]() lt-sec
lt-sec![]() .
.
In the radial dimension I found that the prescription,
![]() constructed a suitable radial profile for the
toroidal field, where
constructed a suitable radial profile for the
toroidal field, where
![]() lt-sec
lt-sec![]() . This
profile is very compact, being nearly constant and non-zero in the
interval
. This
profile is very compact, being nearly constant and non-zero in the
interval ![]() lt-sec, but nearly zero everywhere else.
Here I used 300 terms for both the
lt-sec, but nearly zero everywhere else.
Here I used 300 terms for both the ![]() and
and ![]() terms.
terms.
The following figure shows the geometry of the toroid with respect to the X-Y plane (the iso-surface is about 5% of peak value).
