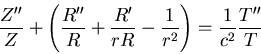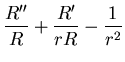

Next: Standing Wave Solution
Up: Maxwell's Equations and a
Previous: Wave Equation in Cylindrical
The differential equation (11) above is commonly solved by
the technique of separation of variables. The basic idea behind this
technique is to assume, initially, that the variable of interest can
be separated into factors which depend separately on the coordinates.
In this case, we assume that  can be expressed as
can be expressed as
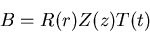 |
(12) |
(again recall that 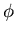 does not enter because of symmetry). I
substitute this equation into the differential equation, and after
dividing once by
does not enter because of symmetry). I
substitute this equation into the differential equation, and after
dividing once by 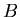 I arrive at
I arrive at
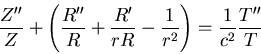 |
(13) |
where the derivatives are with respect to their individual variables.
Now the interesting thing about this technique is that each of the
terms is a function of a different variable,
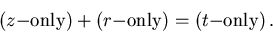 |
(14) |
Therefore, each of the terms must be constant. If one of the
terms was not constant, then there would be no way that the other
terms could compensate, since they depend on different variables.
Thus we can rewrite the equation as
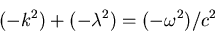 |
(15) |
where 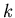 ,
, 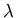 and
and 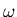 are constants, and
are constants, and
It is worth asking why I inserted negative values rather
than positive values. The answer is that I could have, but these
would lead to solutions which diverge at infinite radius or time, and
thus cannot be physical.


Next: Standing Wave Solution
Up: Maxwell's Equations and a
Previous: Wave Equation in Cylindrical
Craig Markwardt
2001-07-30
![]() can be expressed as
can be expressed as