As pointed out above, the divergence of ![]() is zero, so the wave
equation reduces to
is zero, so the wave
equation reduces to
The particular geometry I am interested in is the initial condition of
a toroidal magnetic flux loop, which is to say, a magnetic field loop
situated on a plane, concentrated between a minor and major radius.
The magnetic field is always toroidal (i.e., in the ![]() direction). Because of this symmetry, I will use cylindrical
coordinates (
direction). Because of this symmetry, I will use cylindrical
coordinates (![]() ,
,![]() ,
,![]() ). In this arrangement the flux loop is
placed in the
). In this arrangement the flux loop is
placed in the ![]() plane, with uniform magnetic field in the
plane, with uniform magnetic field in the
![]() direction. This further simplifies the equations
because, at least initially,
direction. This further simplifies the equations
because, at least initially, ![]() and
and ![]() are zero. Also, we can
assume that derivatives with respect to
are zero. Also, we can
assume that derivatives with respect to ![]() are zero because the
field is azimuthally uniform.
are zero because the
field is azimuthally uniform.
Standard calculus and physics textbooks contain the formulae for
differential operators expressed in cylindrical coordinates. The curl
becomes
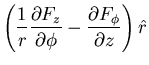 |
(9) | ||
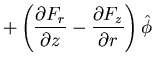 |
|||
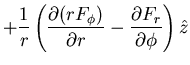 |
The evaluation of this formula appears at first glance to be very
difficult, but because of the symmetry in the initial conditions, we
can set all ![]() and
and ![]() components, and all
components, and all
![]() terms to zero. This leaves only two terms
remaining after performing the curl operation twice:
terms to zero. This leaves only two terms
remaining after performing the curl operation twice:
Substituting back into the modified wave equation
(8), I arrive at this differential equation,