| (1) | |||
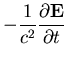 |
(2) | ||
| (3) | |||
| (4) |
Maxwell's equations for a region with no charge or current are, in differential form:
| (1) | |||
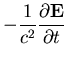 |
(2) | ||
| (3) | |||
| (4) |
Here I have assumed that the the charge density ![]() and current
density
and current
density ![]() are zero, and that the electric displacement vector
can be expressed as
are zero, and that the electric displacement vector
can be expressed as
![]() and the magnetic flux
can be expressed as
and the magnetic flux
can be expressed as
![]() , which are common
assumptions. Thus, the speed
, which are common
assumptions. Thus, the speed ![]() in the equations above refer to the
speed of light in the particular medium
in the equations above refer to the
speed of light in the particular medium
![]() ,
and in the case of a vacuum,
,
and in the case of a vacuum, ![]() is the standard speed of light in
vacuum.
is the standard speed of light in
vacuum.
In this problem I will focus exclusively on the magnetic field
components. Since the above equations are coupled, it suffices to
solve either for the electric field ![]() or magnetic field
or magnetic field ![]() ,
and then the other vector can be inferred. This leads to a set of
vector wave equation:
,
and then the other vector can be inferred. This leads to a set of
vector wave equation: